\( \DeclareMathOperator{\abs}{abs} \)

Not getting wet when it rains

1 Mathematical description of the problem

Sometimes one wonders if when in a thunderstorm the rain comes from behind there is an optimum walking speed that allows to get less wet than normally.:
In order to determine if this is true it is helful to build a small model of yourself that is easily handled with mathematical means

If you happened to be exactly rectangular in shape the top of your head would obviously be hit by an amount of water that depends on the following factors:

(%i1) V_Top:V[Top]=p*v[Rain\,y]*A[Top]*t;
\[\mathrm{\tt (\%o1) }\quad {{V}_{\mathit{Top}}}=p\cdot {{v}_{\mathit{Rain,y}}}\cdot t\cdot {{A}_{\mathit{Top}}}\]

The amount of rain that will hit your front and your back will be zero if you are moving forwards as fast as the rain does and will be higher the more the two speeds deviate from another:

(%i2) V_Sides:V[Sides]=p*abs(v[Rain\,x]-v[Walk\,x])*A[Sides]*t;
\[\mathrm{\tt (\%o2) }\quad {{V}_{\mathit{Sides}}}=p\cdot {{A}_{\mathit{Sides}}}\cdot t\cdot \left| {{v}_{\mathit{Walk,x}}}-{{v}_{\mathit{Rain,x}}}\right| \]

The last calculations can be added up to a total amount of rain per second:

(%i4) V=V[Top]+V[Sides];
V_total:at(%,[V_Top,V_Sides]);
\[\mathrm{\tt (\%o3) }\quad V={{V}_{\mathit{Top}}}+{{V}_{\mathit{Sides}}}\]\[\mathrm{\tt (\%o4) }\quad V=p\cdot {{A}_{\mathit{Sides}}}\cdot t\cdot \left| {{v}_{\mathit{Walk,x}}}-{{v}_{\mathit{Rain,x}}}\right| +p\cdot {{v}_{\mathit{Rain,y}}}\cdot t\cdot {{A}_{\mathit{Top}}}\]

2 One solution

If the main goal is to get less wet in a fixed amount of time there clearly is a solution: Walk exactly as fast as the wind makes the rain move horizontally:

(%i7) Q=V/t;
at(%,V_total);
Q_total:ratsimp(%);
\[\mathrm{\tt (\%o5) }\quad Q=\frac{V}{t}\]\[\mathrm{\tt (\%o6) }\quad Q=\frac{p\cdot {{A}_{\mathit{Sides}}}\cdot t\cdot \left| {{v}_{\mathit{Walk,x}}}-{{v}_{\mathit{Rain,x}}}\right| +p\cdot {{v}_{\mathit{Rain,y}}}\cdot t\cdot {{A}_{\mathit{Top}}}}{t}\]\[\mathrm{\tt (\%o7) }\quad Q=p\cdot {{A}_{\mathit{Sides}}}\cdot \left| {{v}_{\mathit{Walk,x}}}-{{v}_{\mathit{Rain,x}}}\right| +p\cdot {{v}_{\mathit{Rain,y}}}\cdot {{A}_{\mathit{Top}}}\]

The constants that were picked in order to be able to display the following animation were a little bit random, to be honest. But they are good enough to show the fundamental shape of the curves.

(%i8) load("draw")$
\[\mbox{}\\\mbox{;; loading \#P"/home/gunter/.maxima/binary/branch\_5\_36\_base\_188\_g2908479/sbcl/1\_2\_14\_debian/share/draw/grcommon.fasl"}\]\[\mbox{}\\\mbox{;; loading \#P"/home/gunter/.maxima/binary/branch\_5\_36\_base\_188\_g2908479/sbcl/1\_2\_14\_debian/share/draw/gnuplot.fasl"}\]\[\mbox{}\\\mbox{;; loading \#P"/home/gunter/.maxima/binary/branch\_5\_36\_base\_188\_g2908479/sbcl/1\_2\_14\_debian/share/draw/vtk.fasl"}\]\[\mbox{}\\\mbox{;; loading \#P"/home/gunter/.maxima/binary/branch\_5\_36\_base\_188\_g2908479/sbcl/1\_2\_14\_debian/share/draw/picture.fasl"}\]
(%i9) with_slider_draw(
   vr,makelist(i,i,-10,10),
   title=concat("Rain velocity in x-direction:",vr),
   explicit(
      at(
           rhs(Q_total),
           [
               p=.01,
               v[Rain\,y]=20,
               v[Rain\,x]=vr,
               A[Top]=.1,
               A[Sides]=.6
           ]
       ),
       v[Walk\,x],-10,10
   ),
   grid=true,
   yrange=[0,.14],

   ylabel="Amount of water per second",
   xlabel="Walking speed"
)$
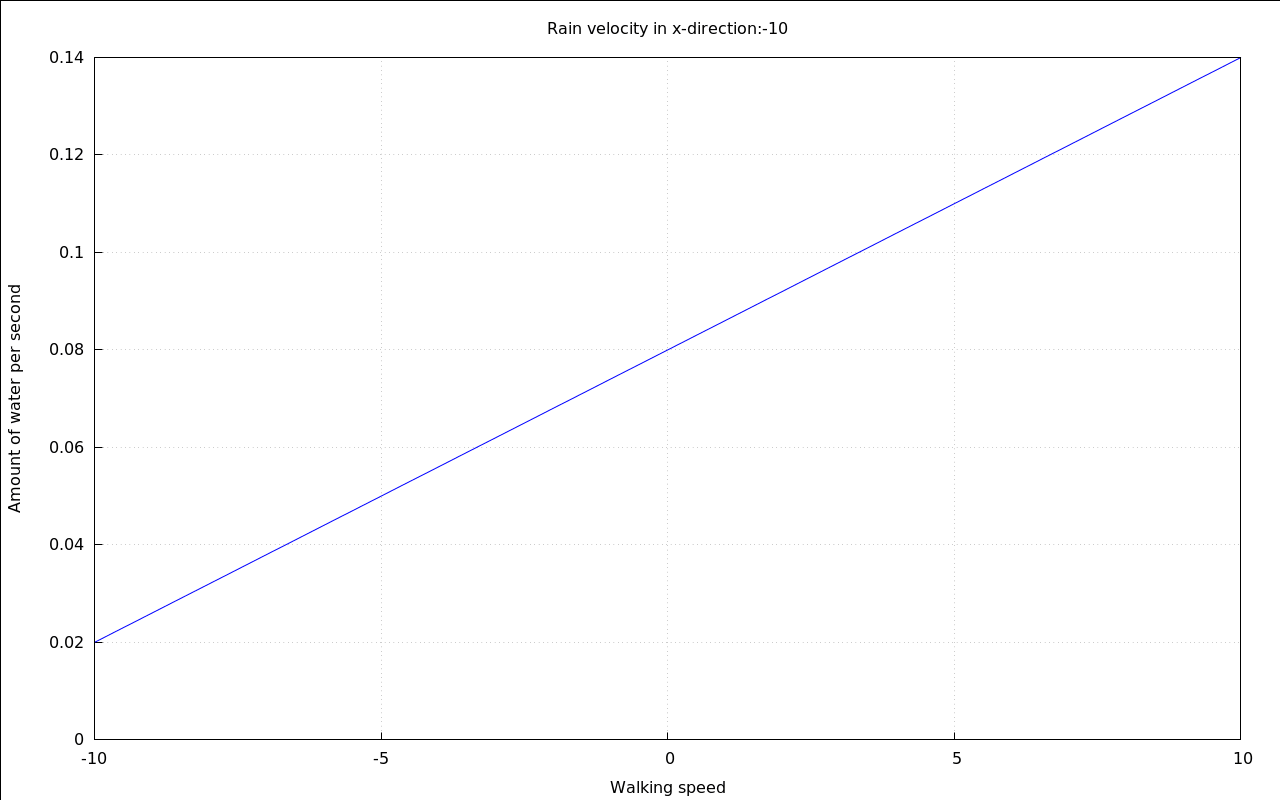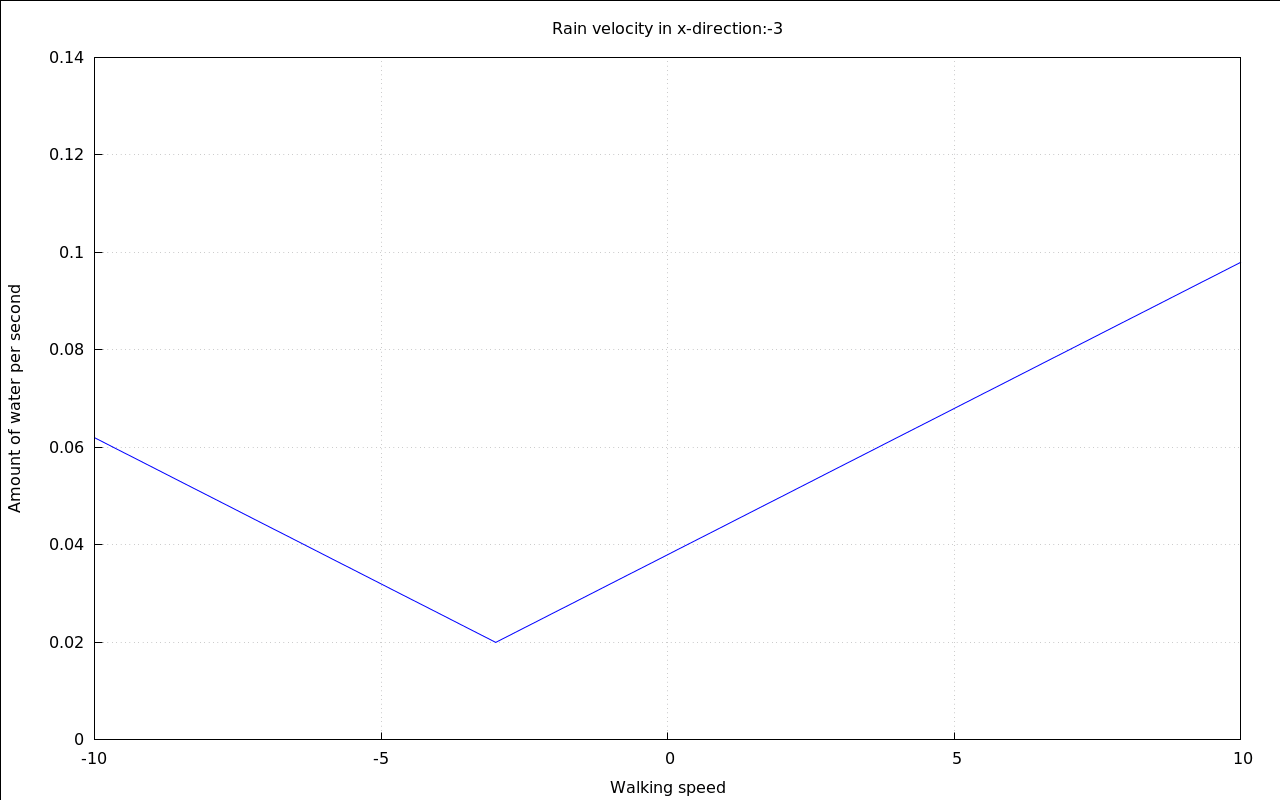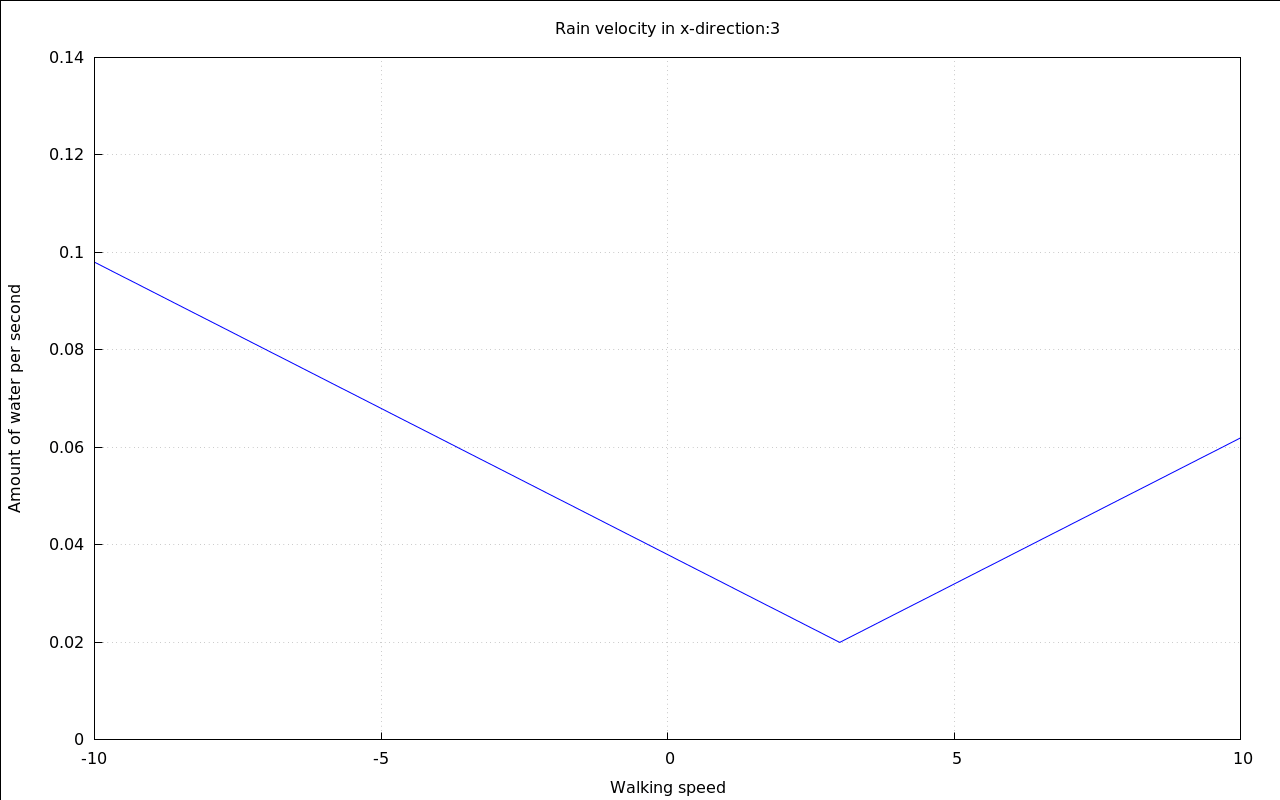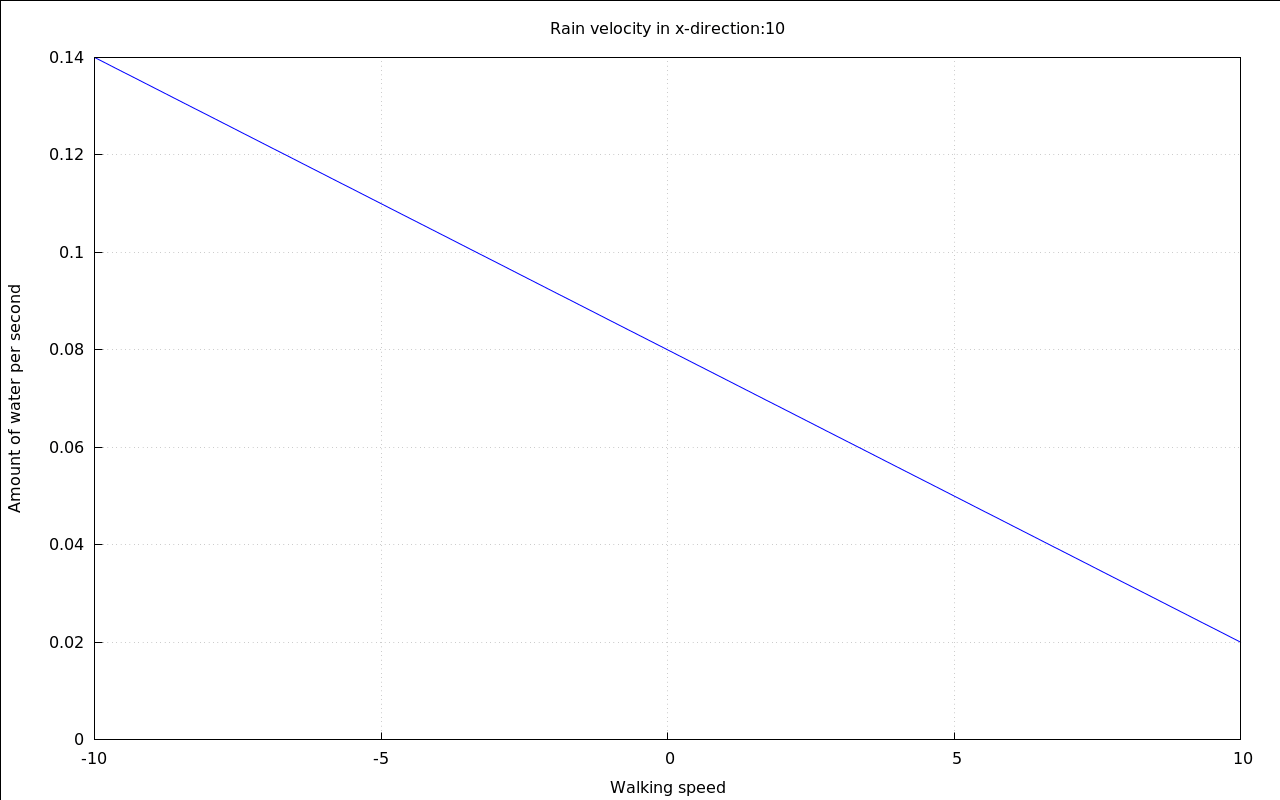
Animated Diagram

3 A second solution

If your aim is to arrive at home at least half-way dry it is the amount of water per meter that counts, not the amount of water per time

The total amount of water after having walked for the distance x is easy to calculate:

(%i12) x=v[Walk\,x]*t;
solve(%,t);
s1:at(V_total,%);
\[\mathrm{\tt (\%o10) }\quad x=t\cdot {{v}_{\mathit{Walk,x}}}\]\[\mathrm{\tt (\%o11) }\quad [t=\frac{x}{{{v}_{\mathit{Walk,x}}}}]\]\[\mathrm{\tt (\%o12) }\quad V=\frac{p\cdot {{A}_{\mathit{Sides}}}\cdot \left| {{v}_{\mathit{Walk,x}}}-{{v}_{\mathit{Rain,x}}}\right| \cdot x}{{{v}_{\mathit{Walk,x}}}}+\frac{p\cdot {{v}_{\mathit{Rain,y}}}\cdot {{A}_{\mathit{Top}}}\cdot x}{{{v}_{\mathit{Walk,x}}}}\]

The amount of water per distance will be calculated by maxima instead:

(%i14) Q='diff(V,x);
Q_perMeter:ev(%,s1,diff);
\[\mathrm{\tt (\%o13) }\quad Q=\frac{d}{d\,x}\cdot V\]\[\mathrm{\tt (\%o14) }\quad Q=\frac{p\cdot {{A}_{\mathit{Sides}}}\cdot \left| {{v}_{\mathit{Walk,x}}}-{{v}_{\mathit{Rain,x}}}\right| }{{{v}_{\mathit{Walk,x}}}}+\frac{p\cdot {{v}_{\mathit{Rain,y}}}\cdot {{A}_{\mathit{Top}}}}{{{v}_{\mathit{Walk,x}}}}\]

This time the meaning of the equation is more difficult to make out:

(%i15) with_slider_draw(
   vr,makelist(i,i,-10,10),
   title=concat("Rain velocity in x-direction:",vr),
   explicit(
       at(
           rhs(Q_perMeter),
           [
               p=.01,
               v[Rain\,y]=20,
               v[Rain\,x]=vr,
               A[Top]=.1,
               A[Sides]=.6

           ]
       ),
       v[Walk\,x],0,10
   ),
   grid=true,
   yrange=[0,2],
 ylabel="Amount of water per second",
   xlabel="Walking speed"
)$
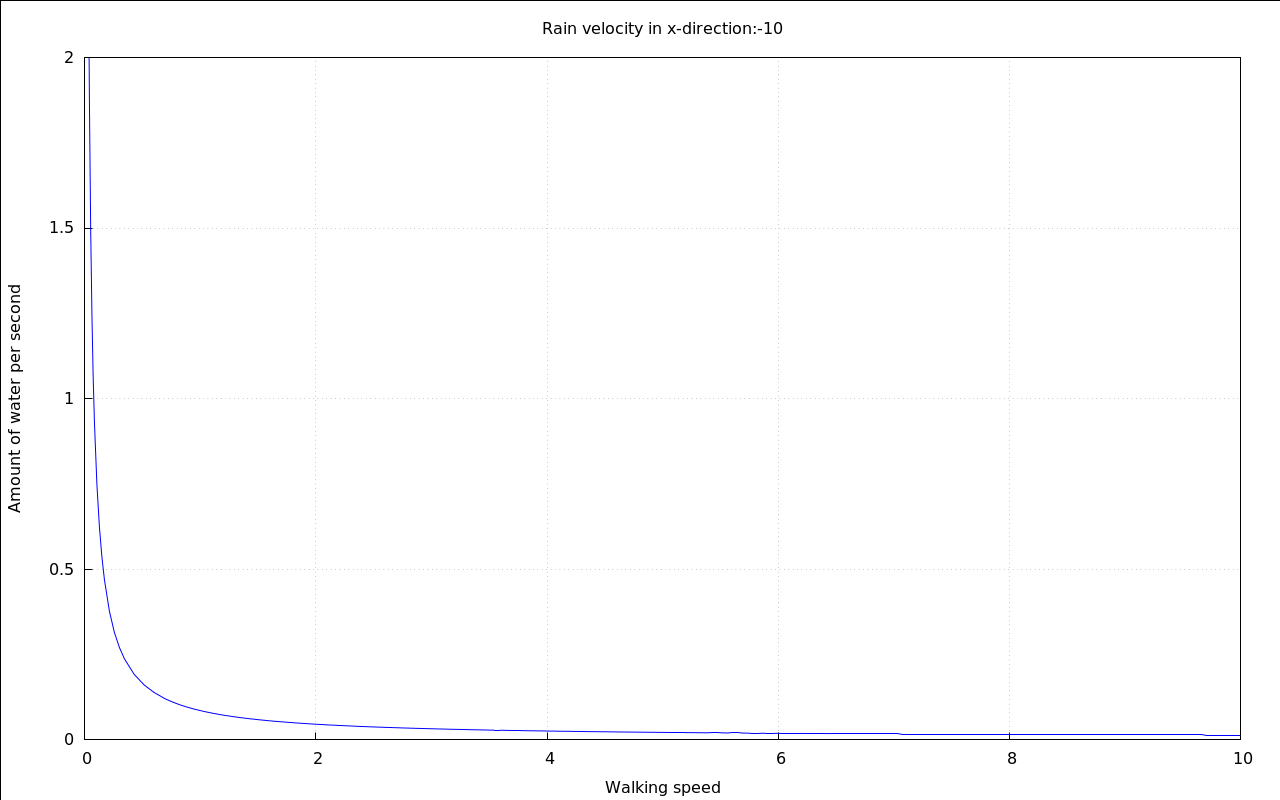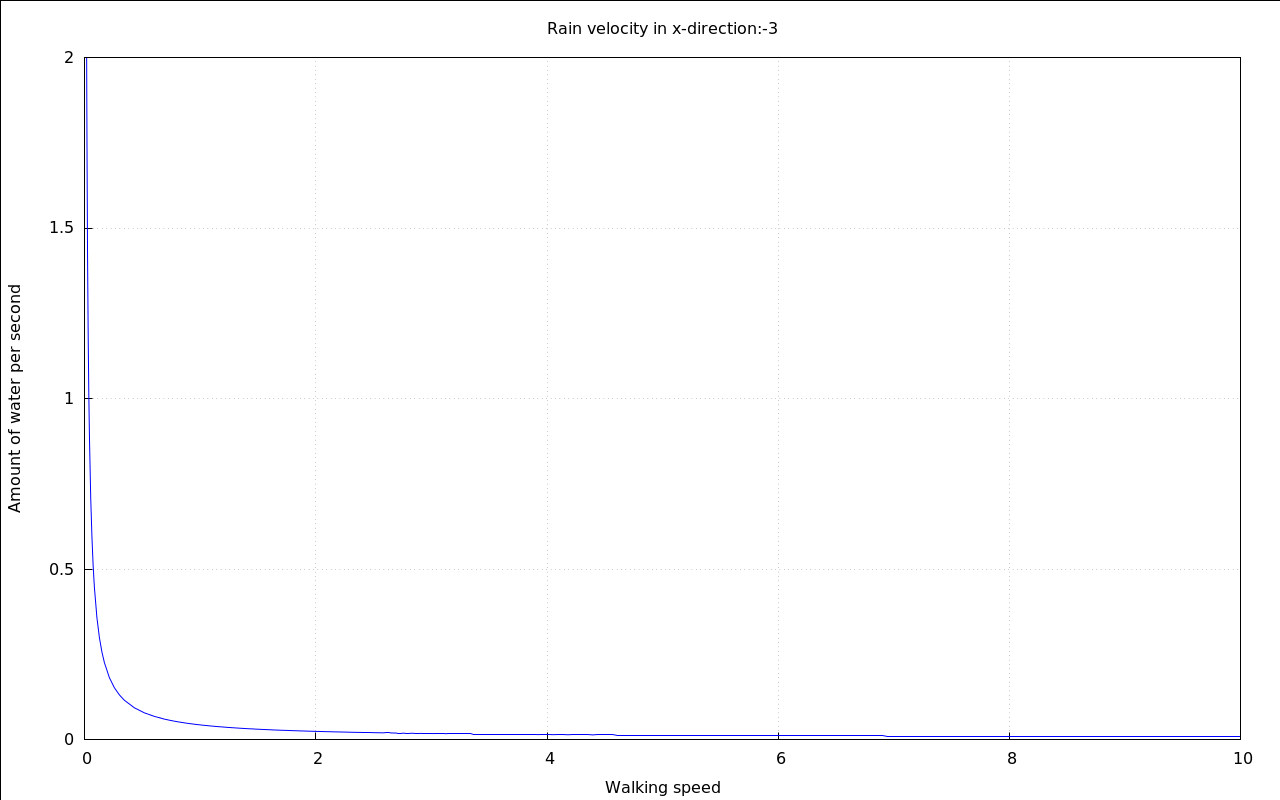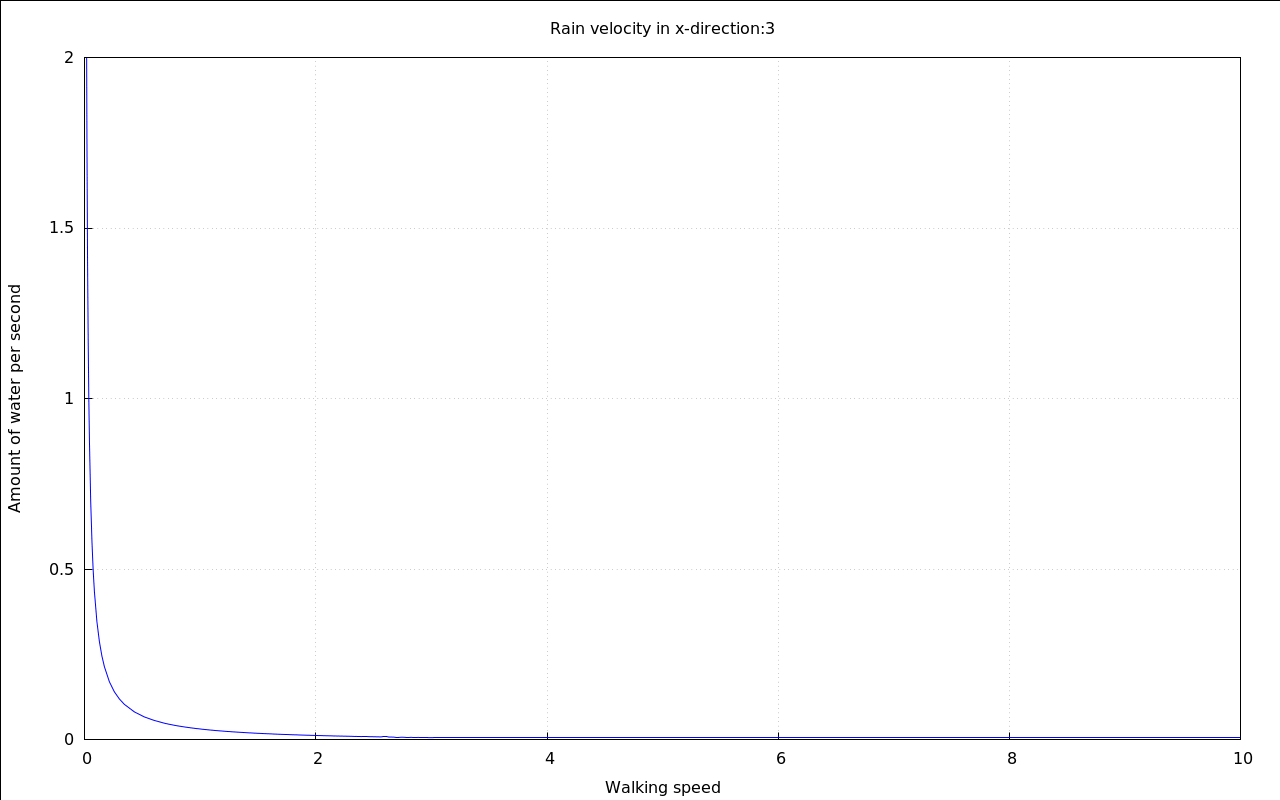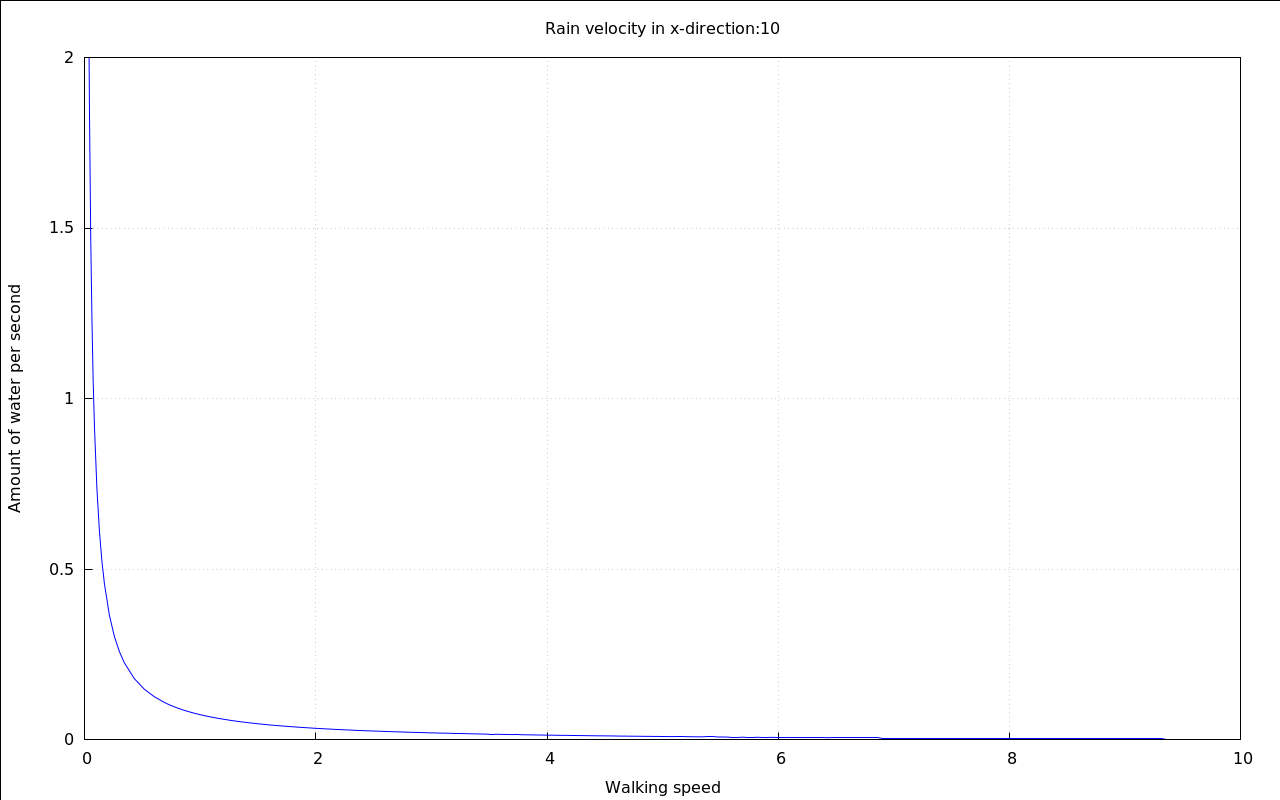
Animated Diagram

The overall shape of the curve shows that if you move too slow you will stay in the rain for too long a time. But wait until we zoom into it:

(%i16) with_slider_draw(
   vr,makelist(i,i,-10,10),
   title=concat("Rain velocity in x-direction:",vr),
   explicit(
       at(
           rhs(Q_perMeter),
           [
              p=.01,
               v[Rain\,y]=20,
               v[Rain\,x]=vr,
               A[Top]=.1,
               A[Sides]=.6
           ]
       ),
       v[Walk\,x],0,60
   ),
   grid=true,
   yrange=[0,.04],
   ylabel="Amount of water per second",
   xlabel="Walking speed"
)$
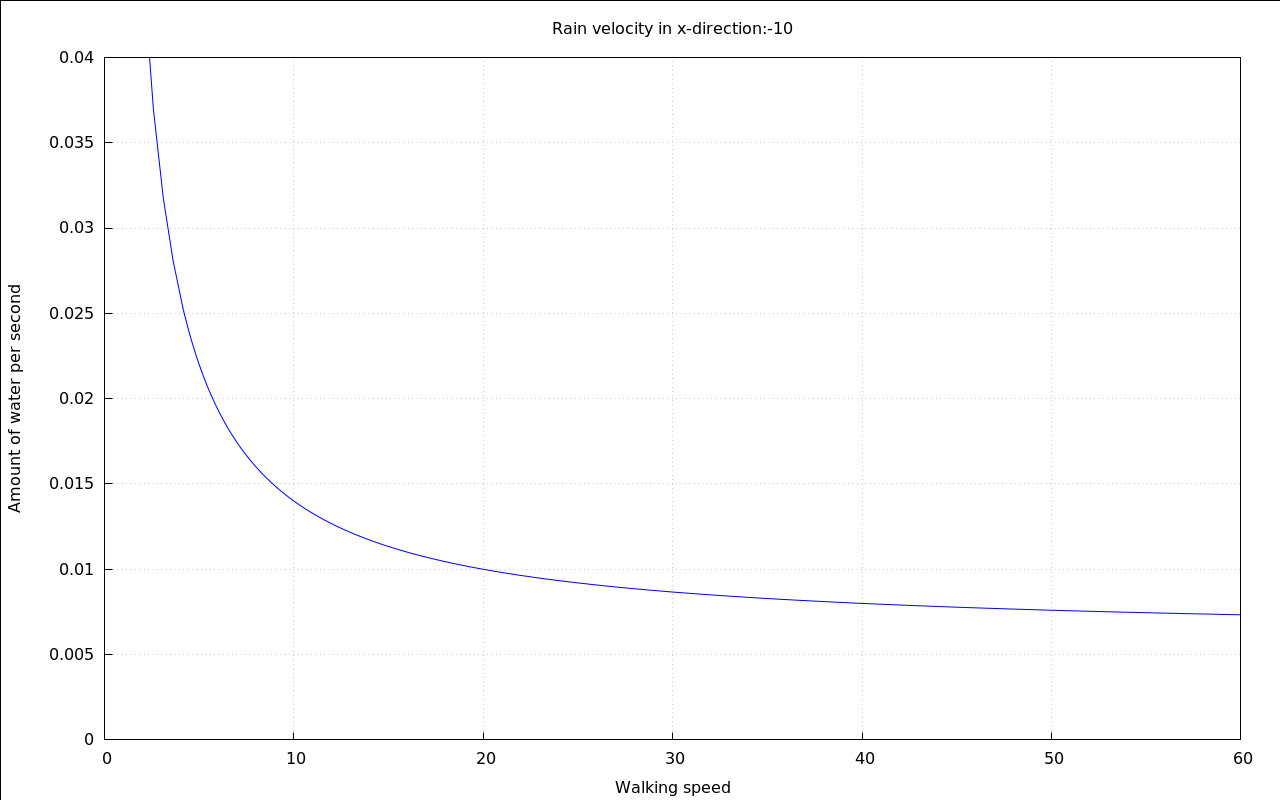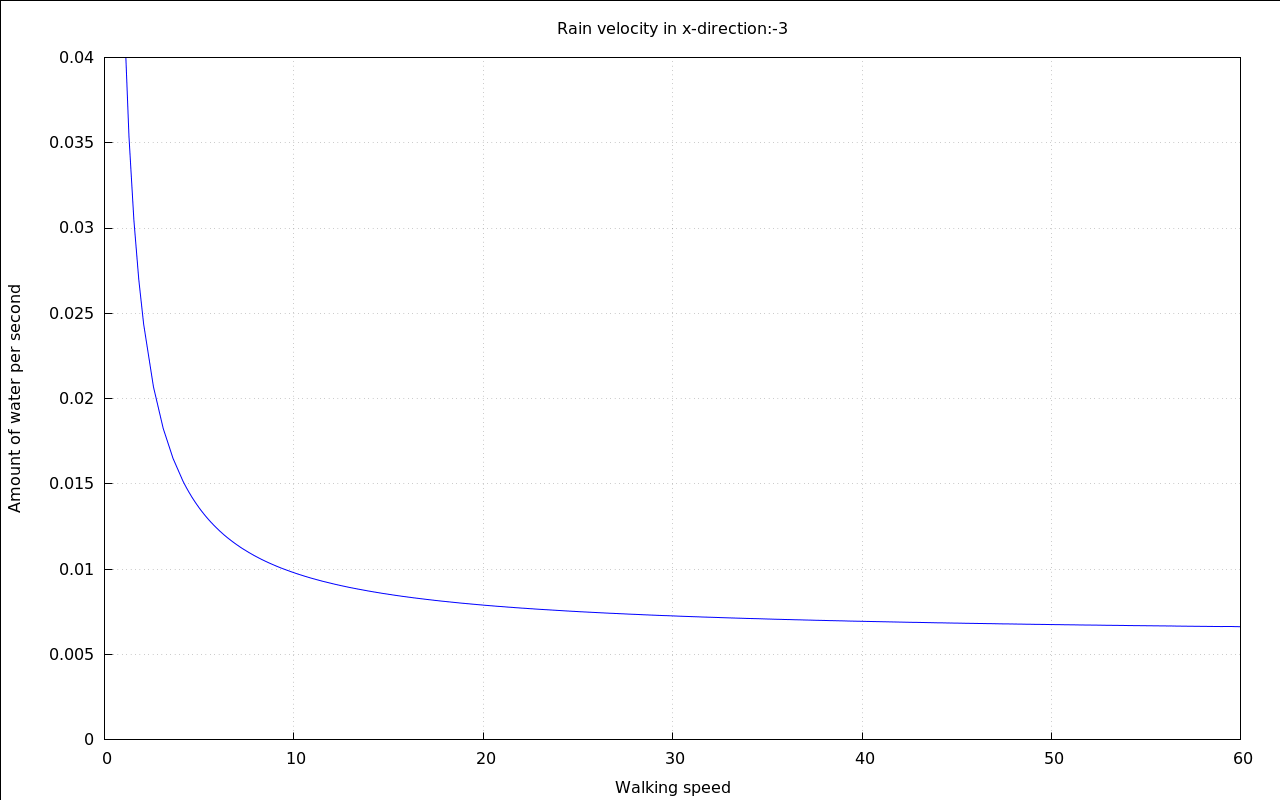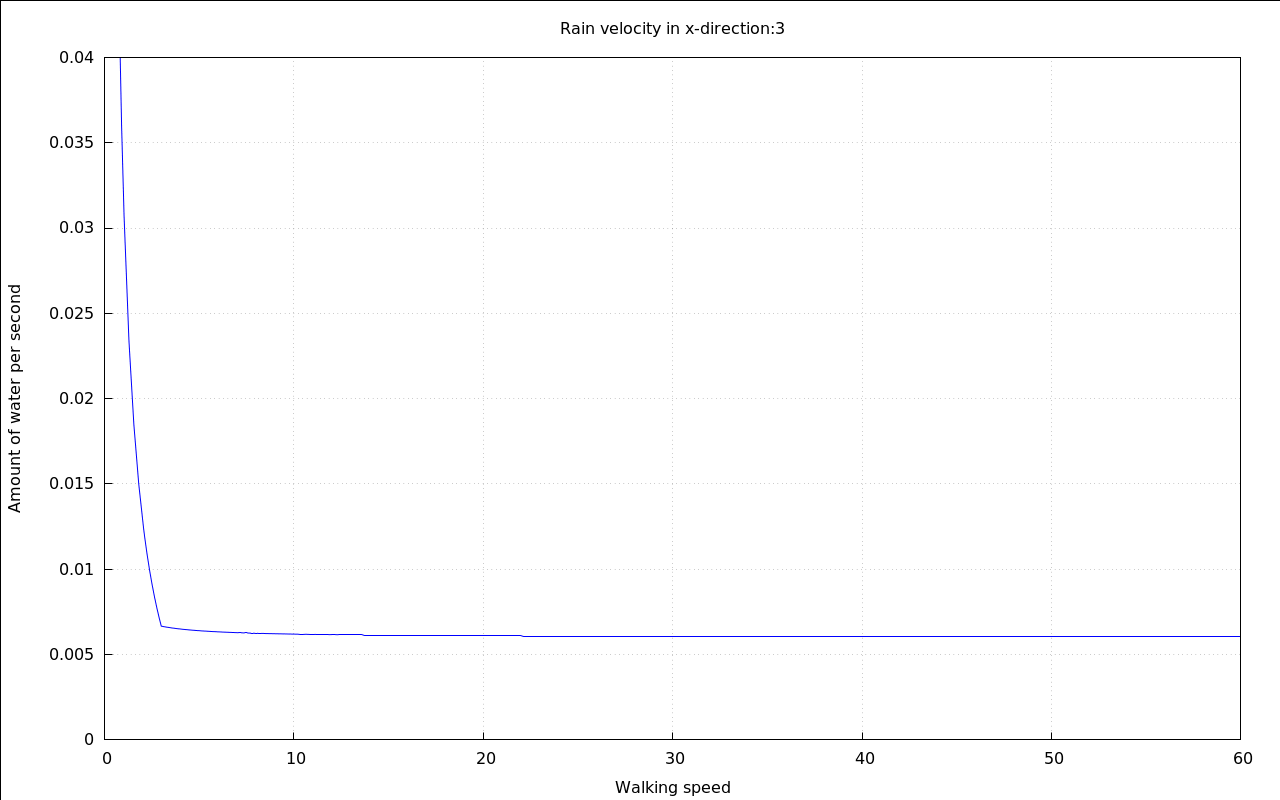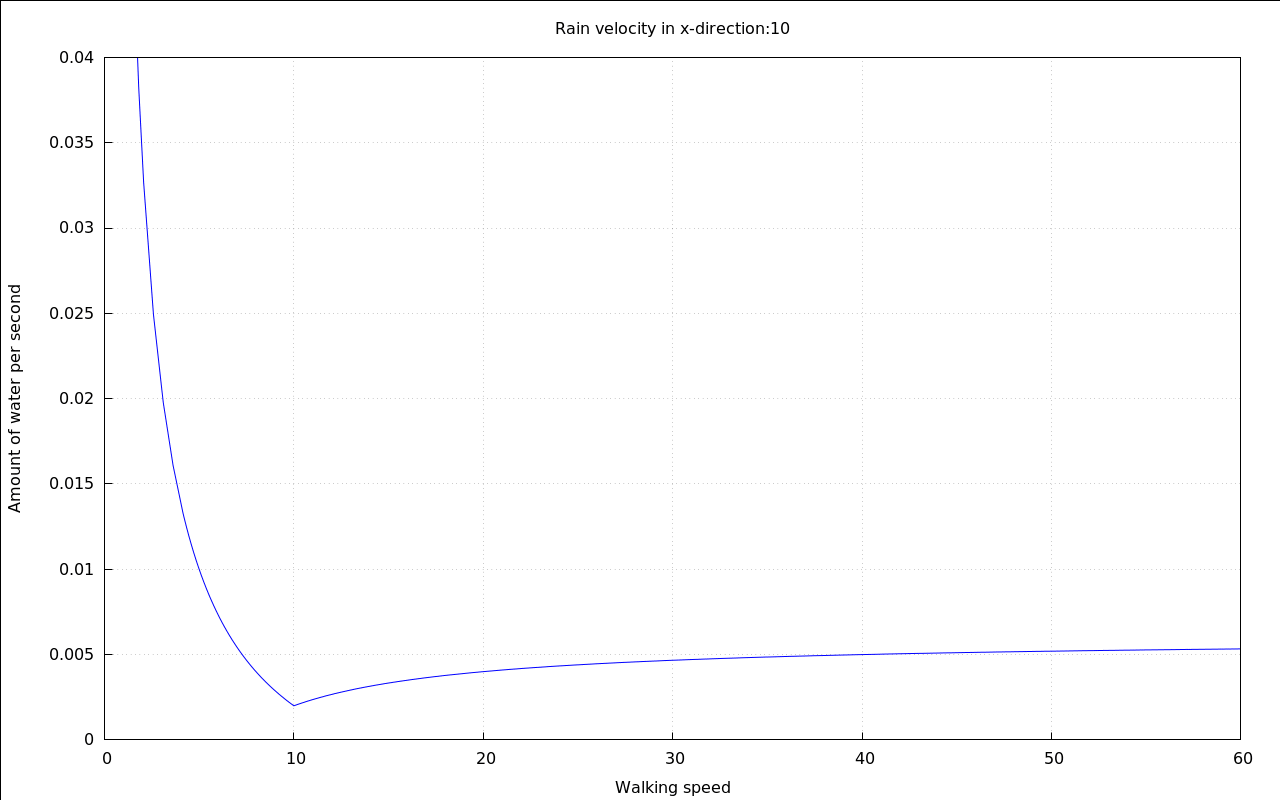
Animated Diagram

It seems that this time there is a optimum speed, too - if the rain is falling horizontally enough.

4 The total amount of water in a given distance

Just to make this document contain a nice integral sign:

(%i17) V[Water]=integrate(Q[Rain](x),x,0,Distance);
\[\mathrm{\tt (\%o17) }\quad {{V}_{\mathit{Water}}}=\int_{0}^{\mathit{Distance}}{{Q}_{\mathit{Rain}}}\left( x\right) dx\]

5 Credits

Special Thanks to Robin Lehmann and Marco Juresic for asking this question in 1996!

This file was generated by the HTML export of a post-15.04 wxMaxima with MathJAX enabled.

Created with wxMaxima. The source of this maxima session can be downloaded here.